Sorting puts the elements of a list in a certain order. It’s important to understand and optimize sorting algorithms as it is used in various other algorithms which require their input data to be sorted. Sorting algorithms are essential in a broad variety of applications including obvious ones like in the organization of a music library, binary search in a database to non-obvious ones in computer graphics and load balancing on a parallel computer. 

Which algorithm to use?

There are several sorting algorithms available for us to use. We might think Java’s system sort is solid for all applications but turns out to be No! It can take quadratic time or even crash for certain killer inputs. It is important to choose the right sorting algorithm for our use case depending on various attributes like:

• Stable? In-place?
• Parallel? 
• Need guaranteed performance?
• Distinct keys?
• Is your list randomly ordered?
• Linked lists or arrays?
• Size of input

A good combination of these attributes can be useful in choosing the right algorithm. At the end of this blog, I have summarized various sorting algorithms based on these factors. Full code of all the below algorithms can be found on Github.

Selection sort

It scans from left to right starting from 0th position, finding the smallest item to the right of the current position and then swap with the current element. 

public void sort(int[] arr) {
    int N = arr.length;
    for (int i = 0; i < N; i++) {
        int minIndex = i;
        for (int j = i + 1; j < N; j++) {
            if (less(arr[j], arr[minIndex])) {
                minIndex = j;
            }
        }
        swap(arr, i, minIndex);
    }
}

Starting the pointer i from 0, moves i to right, identifies the index of least element minIndexon right and swaps it into the current position. 

Complexity

It uses N²/2 compares and N swaps making it a quadratic algorithm irrespective of input. 

Insertion sort

Idea: In the iteration i, all elements to the left of i will be sorted. When it expands with with a new element at position i, it should be inserted at the right position in sorted left part. So it loops through it using counter j and swaps a[i] with larger entry to its left. In a loop, 

• Move the pointer i to the right
• Move j from right to left starting from i, swap a[i] with each large item to its left

public void sort(int[] arr) {
    int N = arr.length;
    for (int i = 0; i < N; i++) {
        for (int j = i; j > 0; j--) {
            if (less(arr[j], arr[j - 1])) swap(arr, j, j - 1);
            else break;
        }
    }
}

Complexity

Worst case: Uses N²/2 compares and swaps (when the array is sorted in reverse order)

Best case: N-1 compares and 0 swaps (when already sorted). This is better suited for partially sorted input.

Merge sort

Merge sort is the algorithm used in the sorting of objects in java.util.Arrays.sort() library. It uses divide and conquer technique to sort, with the idea: 

• Divide array into two halves
• Recursively sort each of it
• Merge the two halves

public void sort(int[] arr, int[] aux, int start, int end) {
    if (end == start) return;
    int mid = (start + end) / 2;

    sort(arr, aux, start, mid);
    sort(arr, aux, mid + 1, end);
    merge(arr, aux, start, mid, end);
}

Once we have two sorted arrays, merge can be done by having pointers at beginning of each and copying over the smaller item to new array to get sorted array until we reach the end of each array. 

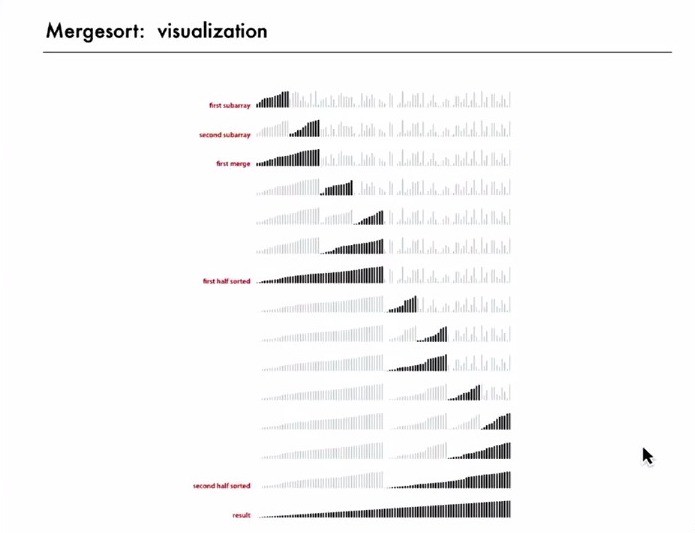
Merge sort visualization. You can clearly see the divide and conquer technique used here. Image Source: Coursera

Complexity

Time: Uses utmost N log N compares and 6N log N array accesses to sort any array.

Space: Uses extra space proportional to N, for the auxiliary array.

Optimizations

• Use insertion sort for smaller array sizes, say ~ 7
• Avoid merge process if already sorted. If the biggest element of left subarray is less than the smallest element of the right subarray, there is no need to a merge.

Quick sort

This algorithm is used in the sorting of primitive types in Arrays.sort() of java.util library. 

Idea: 

• Shuffle array(required for performance gains)
• Partition it such that for some index k, arr[k] is in place, all entries to the left of k are smaller than arr[k] and all entries to the right of k are greater than arr[k]
• Sort each piece recursively

public void sort(int[] arr) {
    StdRandom.shuffle(arr);
    sort(arr, 0, arr.length - 1);
}

private void sort(int[] arr, int start, int end) {
    if (end <= start) return;

    int partitionIndex = partition(arr, start, end);
    sort(arr, start, partitionIndex - 1);
    sort(arr, partitionIndex + 1, end);
}

private int partition(int[] arr, int low, int high) {
    int i = low, j = high + 1;
    while (true) {
        while (less(arr[++i], arr[low])) if (i == high) break;
        while (less(arr[low], arr[--j])) if (j == low) break;
        if (i >= j) break;

        swap(arr, i, j);
    }
    swap(arr, low, j);
    return j;
}

It does more number of compares than merge sort, but this is faster because of less data movement. Quick sort is in-place, but not stable sorting algorithm.

Time Complexity

Best case: N lg N compares

Worst case: N²/2 compares (quadratic)

Average case: ~1.39 N lg N 

3-way Partitioning

Quicksort takes quadratic time to sort items with duplicates. The 3-way partition can perform better than that. Idea is to partition array into 3 parts such that:

• Entries between lt and gt are all equal to partition item
• Entries to the left of lt are less than partition item
• Entries to the right of gt are greater than partition item

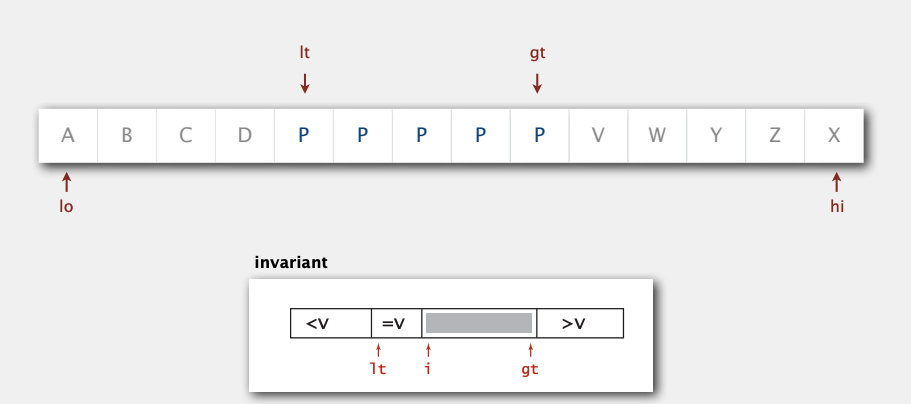3-way partitioning. Source: Coursera

If a[lo] is partition item v,

• a[i] < v, swap v and a[i], increment i and lt
• a[i] > v, swap a[i] and a[gt], decrement gt
• a[i] == v, increment i 

public void sort(int[] arr) {
    sort(arr, 0, arr.length - 1);
}
private void sort(int[] arr, int low, int high) {
    if (low >= high) return;
    int lt = low, i = low, gt = high;
    while(i <= gt) {
        if (arr[i] < arr[lt]) {
            swap(arr, lt, i);
            lt++; i++;
        } else if (arr[i] > arr[lt]) {
            swap(arr, gt, i);
            gt--;
        } else i++;
    }
    sort(arr, low, lt-1);
    sort(arr, gt+1, high);
}

Efficiency

It is entropy optimal. Linear in many cases.

Summary

With so many sorting algorithms present out there, it’s definitely worthwhile to understand the pros and cons of each of it and use it according to our use case to obtain the best performance. Quicksort, fastest in practice and Merge sort which is a stable algorithm are the most popular ones. A simple in-place, stable, N log N guaranteed algorithm is yet to be seen. 

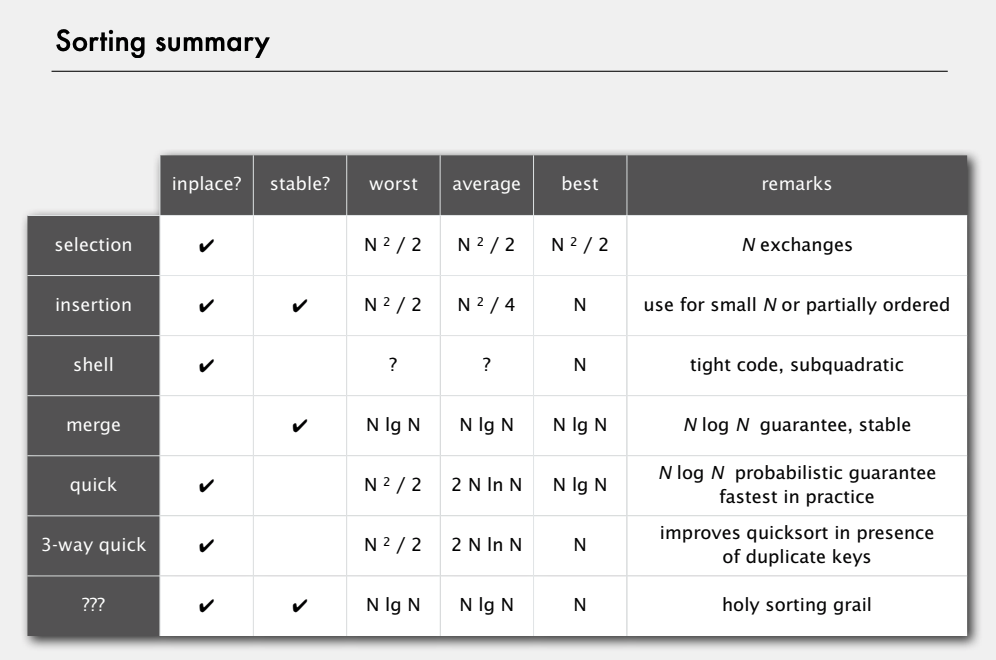Summary of various sorting algorithms. Source: Coursera

Implementation of all of these algorithms in Java can be found on my Github: https://github.com/apoorvam/algorithms/tree/master/src/sorting

This video on the visualization of various sorting algorithms helps to get a better understanding.

Thanks for reading!